T1 线段
题意
$n$ 个区间，从其中选出 $m$ 个，使得全部 $m$ 个线段交非空。求这 m 个线段长度极差的最小值。
\[m\le n \le 5\times 10^5\]思路
线段按长度排序，随后双指针。开线段树表示每个位置被覆盖次数，最大值大于 $m$ 时合法。
T2 国王饮水记
(见之前题解)
T3 旷野大计算
题意：略
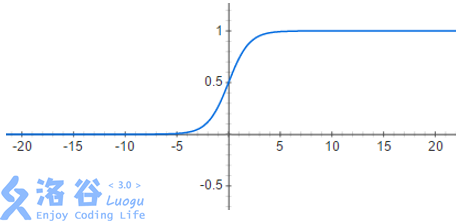
一些关于 $S(x)$ 的性质（注意 S 函数非常有用）：
- $S^\prime(x)=\frac{e^{-x}}{(1+e^{-x})^2}$
- $\lim_{x\to 0}S(x)=\frac 12$
- $\lim_{x\to \infin}S(x)=1$
- $\lim_{x\to -\infin}S(x)=0$
后文中，我们定义 $\infin$ 为一个超级大的数，具体实现时一般用 2 的多少次幂，方便用左移右移搞出来。
Task 1,2：略
Task 3
要求节点数量不超过 6，第一个要动脑筋的地方。
注意到输出不是线性的，因此不用 s 是不可能做到的。然后，我们定义
\[P(x)=S(x\times \infin)=\left\{ \begin{aligned} 1 &\qquad &x>0 \\ 0.5 &&x=0\\ 0 &&x<0 \end{aligned} \right.\]这个 $P$ 函数之后也非常有用，在这里直接 $2P(x)-1$ 即可。
Task 4
14 个节点满分。
6 分
这个 task 满分比较难，在此先使用上问结果乘以 a 得到 6 分。
10 分
（没想出来，只能揣测下出题人思路）
首先，绝对值也不是线性函数，必定会用到 S 函数。然后考虑我们用 S 搞出个什么函数之后我们可以通过平移和线性变换变成绝对值函数。
发现这个函数必然然是一个两段的折线，就是说，存在某个 $x_0$，使得这一函数在 $x<x_0$ 的斜率不等于 $x>x_0$ 时的斜率。
这样，我们可以先把 $x_0$ 平移到 0，然后整体加上某个一次函数，使其变成一个偶函数。最后再整体乘上一个常数，使得其斜率变成 $\pm 1$。
当然，这里也有很多巧合的因素，因为在整体加一次函数和整体乘常数的时候，这个一次函数的斜率和常数都必须非常整，才可以在有限次数中用左移右移凑出来。
考虑如下函数（该函数 0 点的函数值比较麻烦，实现的时候先把输入加上一个 EPS 再做）：
\[f(x)=S(P(x)\times \infin+\frac x {\infin})= \left\{ \begin{aligned} 1&&x>0\cr 0.5+\frac x {4\infin}&&x<0 \end{aligned} \right.\]
这函数是这样的
然而这个函数在并不是一个折线，两个一次函数在 $x=0$ 除没有连起来。然而不要紧，我们可以在最后通过 $P$ 函数把正半轴的函数值全都加上某个数，因此作如下变换：
\[g(x)=(0.5-f(x))\times 8\infin= \left\{ \begin{aligned} -0.5\times 8\infin&&x>0\cr -2x &&x<0 \end{aligned} \right.\]至于为啥把 $x<0$ 弄成 -2x，这是因为后面直接把这个玩意 $+x$，这样正负部分的斜率都对了。然后再使用 $P$ 函数把正半轴的截距搞到 0 即可。实现时注意不要重复计算，精细实现即可满分。
data x = read();
data p = s((x + 1e-20) << 100) << 102; //非零
data r1 = s((x >> 100) + p); // x>=0等于1，x<0等于x>>102+0.5
data r2 = (-r1 + 0.5) << 103; // x>=0等于-0.5*2^103,x<0等于-2x
data r3 = x + r2 + p; //大于0的时候加上2^102
prt(r3);
Task 5
要求95次操作。
模拟即可，需要精细实现，不该加的时候不要乱加。
Task 6
要求190次操作。
从高向低枚举每一位，输出 $P(x-2^i+0.5)$，然后再 $x\gets x- P(x-2^i+0.5)\times 2^i$。
注意到计算 P 的过程中，多次把 x 左移。所以还不如一开始就把 x 左移。
需要精细实现：
data x = read();
x = x << 30;
for (ll i = 31; ~i; i--) {
//减去对应位，判断正负
data res = i ? s(x + (1e6 - powl(2, i + 30))) : x >> 30;
prt(res);
//删除当前位置
if (i) x = x + (-(res << (i + 30)));
}
Task 7
要求600多次操作。
在前两问基础上实现一个异或函数即可。
注意到 $x\oplus y=x+y-2[x+y>1]=x+y-2P(x+y-1.5)$。
Task 8
要求 7 次操作。
一个思路是用二进制把 $\frac 1{10}$ 凑出来，然而七次操作精度太差，只能精确到三位小数。
一个大胆的想法：$S$ 函数的斜率均匀变化，可否找到某处斜率为 $\frac 1{10}$，然后把这段放大放大再放大，用来拟合 $y=\frac x{10}$？
答案是肯定的，一开始你的想法是二分出这个位置，然而：
精度不够。。
求个导：$S^\prime(x)=\frac{e^{-x}}{(1+e^{-x})^2}$，然后算出来这个位置的精确值：$\ln(\sqrt{15}+4)$ 用 C++ 算了一下，输出出来，依然是一个 wa。。
我十分不解，于是翻了翻题解，根据题解的说法，在场上的时候需要用计算器算出小数点后几十位，然后拿程序输出出来才行，于是（第一个数是位置，第二个数是那个位置的 $S$ 函数值）：
string magic = "2.06343706889556054672728117262013187145659144988339249983603269276590284284740991";
data x = (read() >> 100) + magic;
x = S(x) + "-0.887298334620741688517926539978239961083292170529159082658757376611348309193697903351";
prt(x << 100);
就过了，但在考场上大概是看不出这个问题的。。
Task 9
要求 3000 次操作。
自然的想法是插入或冒泡排序。因此，我们需要设计一个模块，输入两个数，这个模块把这两个数按大小顺序排好输出出来。
只要知道了 $\max(x,y)$，也就是第二个数，那么第一个数一减就出来了。
因为 $\max(x,y)=x+\max(y-x,0)$，我们需要设计一个模块，把某个数和 0 取 max。
发现 $y=\max(x,0)$ 的函数竟跟刚刚算绝对值构造的函数有几分相似，这里再回顾一下：
\[f(x)=S(P(x)\times \infin+\frac x {\infin})= \left\{ \begin{aligned} 1&&x>0\cr 0.5+\frac x {4\infin}&&x<0 \end{aligned} \right.\]
发现如果我们把 $x$ 当成 $-x$ 带入到这个函数里，再把正半轴上多的东西减掉，用类似刚才 abs 的手法，就能的到 $\max(x,0)$ 的函数，相当于一个阉割版的 abs。
然后就好弄了：
auto mx0 = [](data x) {
x = -x;
data p = s((x + 1e-20) << 100) << 101; //非零
data r1 = s((x >> 100) + p); // x>=0等于1，x<0等于x>>102+0.5
data r2 = (-r1 + 0.5) << 102; // x>=0等于-0.5*2^102,x<0等于-x
data r3 = r2 + p; // x>=0=0,x<0=-x
return r3;
};
auto swp = [&](data &x, data &y) {
data delt = (-x) + y;
data tmp = mx0(delt);
data sum = x + y;
y = x + tmp;
x = sum + (-y);
};
data arr[20];
for (ll i = 1; i <= 16; i++) {
arr[i] = read();
for (ll j = i; j > 1; j--) swp(arr[j - 1], arr[j]);
}
for (ll i = 1; i <= 16; i++) prt(arr[i]);
Task 10
要求 2000 个节点。
两个大数相乘显然不现实，两个大数相取模也不太现实，因此考虑用龟速乘的搞法。我们需要实现一个模块：输入 $x,y(x\in{0,1})$ 输出 $xy$。
猜想这个模块可以写成 $S(ax+by+c)$。
当 x 取 0 时，无论 y 如何变化，结果都不变，但是当 x 取 1 时，y 变化，结果就变化。
- 说明当 x 取 0 时，$S(by+c)$ 的变化率极小，也就是说 $by+c$ 离 0 很远。
- 说明当 x 取 1 时，$S(a+by+c)$ 的变化率比较大，也就是说 $a+by+c$ 离 0 很进。
不难想到，$a+c=0$，且 b 远小于 1 的时候是满足这个条件的。
同样得，用 $P$ 函数把这个玩意得截距搞一下就好了。
接下来还要实现一个取模的模块，参考取模优化的搞法，如果 $x\gets x- [x\ge mod]\times mod$，直接利用上面的乘法模块即可。
最后还需要把被乘数 $y$ 自身取模一遍，依次用取模模块把 y 对 $2^{31}mod,2^{30}mod \cdots$ 取模即可。
（我至今还没调出来）
作者：@ethan-enhe
本文为作者原创，转载请注明出处：本文链接
阅读量: